Boostrapping a Forth in 40 lines of Lua code

• 1. Forth via examples
• 2. Bootstrapping miniforth
• 3. Modes
• 4. Virtual Modes
• 5. A Bytecode for Polynomials
• 6. A Bytecode Language for Propositional Calculus
• 7. (Meta)Lua on Miniforth
• 8. Why Forth?
• Thanks
• Related work
• Bibliography

The real point of this article is to propose a certain way of implementing a Forth virtual machine; let's call this new way “mode-based”. The main loop of a mode-based Forth is just this:

while mode ~= "stop" do modes[mode]() end

In our mode-based Forth, that is implemented in Lua, and that we will refer to as “miniforth”, new modes can be added dynamically very easily. We will start with a virtual machine that “knows” only one mode - “interpret”, that corresponds to (less than) half of the "outer interpreter" of traditional Forths - and with a dictionary that initially contains just one word, that means “read the rest of the line and interpret that as Lua code”; that minimal virtual machine fits in 40 lines of Lua, and is enough to bootstrap the whole system.

But, “Why Forth?”, the reader will ask - “Forth is old and weird, why shouldn't we stick to modern civilized languages, and ignore Forth? What do you still like in Forth?” - My feeling here is that Forth is one of the two quintessential extensible languages, the other one being Lisp. Lisp is very easy to extend and to modify, but only within certain limits: its syntax, given by ‘read’, is hard to change(1). If we want to implement a little language (as in [Bentley]) with a free-from syntax on top of Lisp, and we know Forth, we might wonder that maybe the right tool for that would have to have characteristics from both Lisp and Forth. And this is where Lua comes in - as a base language for building extensible languages.

(Disclaimer: I'm using the term "Forth" in a loose sense through this article. I will say more about this in the last section.)

Any “normal” Forth has an interactive interface where the user types a line, then hits the “return” key, and then the Forth executes that line, word by word, and displays some output; our miniforth does not have an interactive interface, but most ideas still carry on. Here's a very simple program; the normal text is the user input, and the parts with a darker background are the output from the Forth system. Note that “words” are sequences on non-whitespace characters, delimited by whitespace.

5 DUP * . 25 ok

  ( program 1 )

The program above can be “read aloud” as this: “Put 5 on the stack; run ‘DUP’, i.e., duplicate the element on the top of the stack; multiply the two elements on the top of the stack, replacing them by their product; print the element at the top of the stack and remove it from the stack.”

Here's a program that defines two new functions (“words”, in the Forth jargon):

: SQUARE DUP * ; ok
: CUBE DUP SQUARE * ; ok
5 CUBE . 125 ok

  ( program 2 )

It can be read aloud as this:
  Define some new words:
  “SQUARE”: run DUP, then multiply;
  “CUBE”: run DUP, then run SQUARE, then multiply;
Now put 5 on the stack, CUBE it, and print the result.

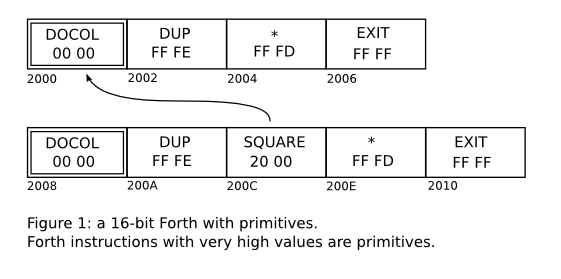
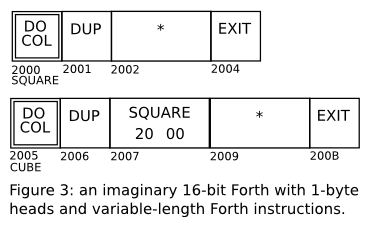
The words SQUARE and CUBE are represented in the memory as some kind of bytecode; different Forths use different kinds of bytecodes. Here we are more interested in “indirect threaded” Forths (see [Ertl]) that store the dictionary in a separate region of the memory. Some possible representations would be like in figures 1, 2, and 3; in these box diagrams all numbers are in hexadecimal, and we are assuming a big-endian machine for simplicity. Figure 4 shows the “bytecode” representation that we will use in miniforth. It is not exactly a bytecode, as the memory cells can hold arbitrary Lua objects, not just bytes - but we will call it a “bytecode” anyway, by abuse of language.

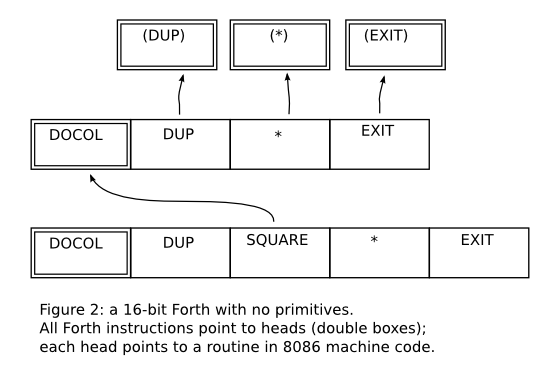
Here's a trace of what happens when we run CUBE (from Program 2 and Figure 4) in miniforth:

RS={ 5 }    mode=head    DS={ 5 }      head="DOCOL"
RS={ 7 }    mode=forth   DS={ 5 }      instr="DUP"
RS={ 8 }    mode=forth   DS={ 5 5 }    instr=1
RS={ 8 1 }  mode=head    DS={ 5 5 }    head="DOCOL"
RS={ 8 3 }  mode=forth   DS={ 5 5 }    instr="DUP"
RS={ 8 4 }  mode=forth   DS={ 5 5 5 }  instr="*"
RS={ 8 5 }  mode=forth   DS={ 5 25 }   instr="EXIT"
RS={ 9 }    mode=forth   DS={ 5 25 }   instr="*"
RS={ 10 }   mode=forth   DS={ 125 }    instr="EXIT"

  Figure 5: a trace of CUBE (Program 2, Figure 4)

Note that we don't have a separate variable for the instruction pointer (IP); we use the top of the return stack (RS) as IP.

The rightmost part of our traces always describe what is going to be executed, while the rest describes the current state. So, in the sixth line we have RS = { 8, 4 }, and we are going to execute the instruction in memory[4], i.e., “*”, in mode "forth".

Program 3a is all that we need to bootstrap miniforth. It defines the main loop (“run”), one mode (“interpret”), the dictionary (“_F”), and one word in the dictionary: “%L”, meaning “evaluate the rest of the current line as Lua code”.

-- Global variables that hold the input:
subj = "5 DUP * ."      -- what we are interpreting (example)
pos  = 1                -- where are are (1 = "at the beginning")

-- Low-level functions to read things from "pos" and advance "pos".
-- Note: the "pat" argument in "parsebypattern" is a pattern with
-- one "real" capture and then an empty capture.
parsebypattern = function (pat)
    local capture, newpos = string.match(subj, pat, pos)
    if newpos then pos = newpos; return capture end
  end
parsespaces     = function () return parsebypattern("^([ \t]*)()") end
parseword       = function () return parsebypattern("^([^ \t\n]+)()") end
parsenewline    = function () return parsebypattern("^(\n)()") end
parserestofline = function () return parsebypattern("^([^\n]*)()") end
parsewordornewline = function () return parseword() or parsenewline() end

-- A "word" is a sequence of one or more non-whitespace characters.
-- The outer interpreter reads one word at a time and executes it.
-- Note that `getwordornewline() or ""' returns a word, or a newline, or "".
getword          = function () parsespaces(); return parseword() end
getwordornewline = function () parsespaces(); return parsewordornewline() end

-- The dictionary.
-- Entries whose values are functions are primitives.
_F = {}
_F["%L"] = function () eval(parserestofline()) end

-- The "processor". It can be in any of several "modes".
-- Its initial behavior is to run modes[mode]() - i.e.,
-- modes.interpret() - until `mode' becomes "stop".
mode  = "interpret"
modes = {}
run = function () while mode ~= "stop" do modes[mode]() end end

-- Initially the processor knows only this mode, "interpret"...
-- Note that "word" is a global variable.
interpretprimitive = function ()
    if type(_F[word]) == "function" then _F[word](); return true end
  end
interpretnonprimitive = function () return false end   -- stub
interpretnumber       = function () return false end   -- stub
p_s_i = function () end  -- print state, for "interpret" (stub)
modes.interpret = function ()
    word = getwordornewline() or ""
    p_s_i()
    local _ = interpretprimitive() or
              interpretnonprimitive() or
              interpretnumber() or
              error("Can't interpret: "..word)
  end

  -- ( Program 3a: the core of miniforth )

Program 3b is a first program in miniforth. It starts with only “%L” defined and it defines several new words: what to do on end-of-line, on end-of-text, and “[L”, that evaluates blocks of Lua code that may span more than one line; then it creates a data stack and defines the words “DUP”, “*”, “5”, and “.”, that operate on it.

-- Our first program in MiniForth.
-- It defines a meaning for newlines (they are no-ops; go ahead),
-- for "" ("at end-of-text, change the mode to 'stop'"),
-- and for "[L" - read everything until a "L]", and interpret
-- what is between the "[L" and the "L] as Lua code, with eval.
-- Then it creates a data stack ("DS") and four words - "5", "DUP",
-- "*", "." - that operate on it.
--
subj = [=[
%L _F["\n"] = function () end
%L _F[""]   = function () mode = "stop" end
%L _F["[L"] = function () eval(parsebypattern("^(.-)%sL]()")) end
[L
  DS = { n = 0 }
  push = function (stack, x) stack.n = stack.n + 1; stack[stack.n] = x end
  pop  = function (stack) local x = stack[stack.n]; stack[stack.n] = nil;
                          stack.n = stack.n - 1; return x end
  _F["5"]   = function () push(DS, 5) end
  _F["DUP"] = function () push(DS, DS[DS.n]) end
  _F["*"]   = function () push(DS, pop(DS) * pop(DS)) end
  _F["."]   = function () io.write(" "..pop(DS)) end
L]
]=]

-- Now run it. There's no visible output.
pos = 1
mode = "interpret"
run()

-- At this point the dictionary (_F) has eight words.

   -- ( Program 3b: a first program in miniforth )

After running Program 3b the system is already powerful enough to run simple Forth programs like, for example,

5 DUP * .

Note that to “run” that what we need to do is:

subj = "5 DUP * ."; pos = 1; mode = "interpret"; run()

It is as if we were setting the memory (here the “subj”) and the registers of a primitive machine by hand, and then pressing its “run” button; clearly, that could be made better, but here we have other priorities.

The Programs 3a and 3b don't have support for non-primitives; this will have to be added later. Look at Figure 4; non-primitives, like “SQUARE”, are represented in the bytecode as numbers - addresses of heads in the memory[] - and we have not introduced neither the memory yet, nor the states “head” or “forth”.

Note that the names of non-primitives do not appear in the memory, only in the dictionary, _F. For convenience in such memory diagrams we will draw the names of non-primitives below their corresponding heads; in Figure 4 _F["SQUARE"] = 1 and _F["CUBE"] = 5.

When the inner interpret runs - i.e., when the mode is "head" or "forth"; see Figure 5 -, at each step the processor reads the contents of the memory at IP and processes it. When the outer interpreter runs, at each step it reads a word from subj starting at pos, and processes it. There's a parallel between these behaviors...

I have never seen any references to "modes" in the literature about Forth. In the usual descriptions of inner interpreters for Forth the "head" mode is not something separate; it is just a transitory state that is part of the semantics of executing a Forth word. And the "interpret" and "compile" modes also do not exist - the outer interpreter is implemented as a Forth word containing a loop; it reads one word at a time, and depending on the value of a variable, STATE, it either "interprets" or "compiles" that word. So, in a sense, "interpret" and "compile" are "virtual modes"...

Let me explain how I arrived at this idea of "modes" - and what I was trying to do that led me there.

Some words interfere in the variables of the outer interpreter. For example, ":" reads the word the pos is pointing at - for example, "SQUARE" -, adds a definition for that word ("SQUARE") to the dictionary, and advances pos; when the control returns to modes.interpret() the variable pos is pointing to the position after SQUARE - and modes.interpret() never tries to process the word SQUARE. Obviously, this can be used to implement new languages, with arbitrary syntax, on top of Forth.

Some words interfere on the variables of the inner interpreter - they modify the return stack. Let's use a more colorful terminology: we will speak of words that “eat text” and of words that “eat bytecode”. As we have seen, “:” is a word that eats text; numerical literals are implemented in Forth code using a word, LIT, that eats bytecode. In the program below,

: DOZENS 12 * ; ok
5 DOZENS . 60 ok

  ( Program 4 )

the word DOZENS is represented in bytecode in miniforth as:

memory = {"DOCOL", "LIT", 12, "*", "EXIT"}
       -- 1        2      3   4    5
       -- DOZENS

  Figure 6: the bytecode for DOZENS (Program 4)

When the LIT in DOZENS executes it reads the 12 that comes after it, and places it on the data stack; then it changes the return stack so that in the next step of the main loop the IP will be 4, not 3. Here is a trace of its execution; note that there is a new mode, "lit". The effect of "executing" the 12 in memory[3] in mode "lit" is to put the 12 in DS.

RS={ 1 }  mode=head   DS={ 5 }     head="DOCOL"
RS={ 2 }  mode=forth  DS={ 5 }     instr="LIT"
RS={ 3 }  mode=lit    DS={ 5 }     data=12
RS={ 4 }  mode=forth  DS={ 5 12 }  instr="*"
RS={ 5 }  mode=forth  DS={ 60 }    instr="EXIT"

  Figure 7: the trace for 5 DOZENS (Program 4, Figure 6)

The code in Lua for the primitive LIT and for the mode lit can be synthesized from the trace. By analyzing what happens between steps 2 and 3 and 3 and 4, we see that LIT and lit must be:

_F["LIT"] = function () mode = "lit" end
modes.lit = function ()
    push(DS, memory[RS[RS.n]])
    RS[RS.n] = RS[RS.n] + 1
    mode = "forth"
  end

so from this point on we will consider that the traces give enough information, and we will not show the corresponding code.

Note that different modes read what they will execute from different places: head, forth and lit read from memory[RS[RS.n]] (they eat bytecode); interpret and compile read from subj, starting at pos (they eat text). Our focus here will be on modes and words that eat bytecode.

How can we create words that eat bytecode, like LIT, in Forth? In the program in Figure 8 the word TESTLITS call first LIT, then VLIT; VLIT should behave similarly to LIT, but LIT is a primitive and VLIT is not.

memory = {"DOCOL", "R>P", "PCELL", "P>R", "EXIT",
      --  1        2      3        4      5
      --  VLIT <---------------\
      --                      |
          "DOCOL", "LIT", 123, 1, 234, "EXIT",}
      --  6        7      8    9  10   11
      --  TESTLITS

  Figure 8: a word (TESTLITS) that uses both LIT and VLIT

t=0  RS={ 6 }     mode=head    PS={  }    DS={  }         head="DOCOL"
t=1  RS={ 7 }     mode=forth   PS={  }    DS={  }         instr="LIT"
t=2  RS={ 8 }     mode=lit     PS={  }    DS={  }         data=123
t=3  RS={ 9 }     mode=forth   PS={  }    DS={ 123 }      instr=1
t=4  RS={ 10 1 }  mode=head    PS={  }    DS={ 123 }      head="DOCOL"
t=5  RS={ 10 2 }  mode=forth   PS={  }    DS={ 123 }      instr="R>P"
t=6  RS={ 3 }     mode=forth   PS={ 10 }  DS={ 123 }      instr="PCELL"
t=7  RS={ 4 }     mode=pcell   PS={ 10 }  DS={ 123 }      pdata=234
t=8  RS={ 4 }     mode=forth   PS={ 11 }  DS={ 123 234 }  instr="P>R"
t=9  RS={ 11 5 }  mode=forth   PS={  }    DS={ 123 234 }  instr="EXIT"
t=10 RS={ 11 }    mode=forth   PS={  }    DS={ 123 234 }  instr="EXIT"

  Figure 9: a trace of TESTLITS (Figure 8)

Figures 8 and 9 contain a full solution, so start by ignoring the cells 2, 3, and 4 of the memory, and the lines t=5 to t=8 of the trace. From t=5 to t=9 what we need to do is

push(DS, memory[RS[RS.n - 1]])
RS[RS.n - 1] = RS[RS.n - 1] + 1

where the -1 is a magic number: roughly, the number of “call frames” in the stack between the call to VLIT and the code that will read its literal data, negated. In other situations this could be -2, -3... One way to get rid of that magic number is to create a new stack - the “parsing stack” (“PS”) - and to have “parsing words” that parse bytecode from the position that the top of PS points to; then a word like VLIT becomes a variation of a word, PCELL, that reads a cell from memory[PS[PS.n]] and advances PS[PS.n]. The code for VLIT in Figure 8 shows how that is done - we wrap PCELL as “R>P PCELL P>R” - and from the trace in Figure 9 we can infer how to define these words.

Note that the transition from t=2 to t=3 corresponds to the transition from t=4 to t=10; the mode being "lit" corresponds to having the address of the head of VLIT at the top of RS, and the mode being "head"; using this idea we can implement virtual modes in Forth. Better yet: it all becomes a bit simpler if we regard the mode as being an invisible element that is always above the top of RS. So, an imaginary mode "vlit" would be translated, or expanded, into a 1 (the head of VLIT), plus a mode "head"; or another word, similar to VLIT, would just switch the mode to "vlit", and the action of that word would be to expand it into the head of VLIT, plus the mode "head".

A polynomial with fixed numerical coefficients can be represented in memory as first the number of these coefficients, then the value of each of them; for example, P(x) = 2x^3 + 3x^2 + 4x + 5.5 is represented as { ..., 4, 2, 3, 4, 5.5, ... }. We will call this representation - number of coefficients, then coefficients - the “data of the polynomial”. Let's start with a primitive, PPOLY, that works like PCELL, in the sense that it reads the data of the polynomial from the memory, starting at the position PS[PS.n], and advancing PS[PS.n] at each step. This PPOLY takes a value from the top of the data stack - it will be 10 in our examples - and replaces it by the result of applying P on it - P(10), which is 2345.5.

By defining POLY from PPOLY, as we defined VLIT from PCELL in Figure 8,

: POLY R>P PPOLY P>R ;

we get a word that eats bytecode; a call to POLY should be followed by data of a polynomial, just like LIT is followed by a number. And we can also do something else: we can create new heads, DOPOLY and DOADDR, and represent polynomials as two heads followed by the data of the polynomial. The program in Figure 10, that tests this idea, has the trace in Figure 11.

memory = {"DOPOLY", "DOADDR", 4, 2, 3, 4, 5.5,
      --  1         2         3  4  5  6   7
      --  P(X)      &P(X)
      --  ^---------------------\
      --                        |
          "DOCOL",   "LIT", 10, 1, "EXIT"}
      --  8          9      10  11 12
      --  TESTDOPOLY

  ( Figure 10: put 10 on the stack, call P(X) )

RS={ 8 }         mode=head    PS={  }   DS={  }        head="DOCOL"
RS={ 9 }         mode=forth   PS={  }   DS={  }        instr="LIT"
RS={ 10 }        mode=lit     PS={  }   DS={  }        data=10
RS={ 11 }        mode=forth   PS={  }   DS={ 10 }      instr=1
RS={ 12 1 }      mode=head    PS={  }   DS={ 10 }      head="DOPOLY"
RS={ 12 forth }  mode=ppolyn  PS={ 3 }  DS={ 10 }      n=4
RS={ 12 forth }  mode=ppolyc  PS={ 4 }  DS={ 10 }      n=4 acc=0 coef=2
RS={ 12 forth }  mode=ppolyc  PS={ 5 }  DS={ 10 }      n=3 acc=2 coef=3
RS={ 12 forth }  mode=ppolyc  PS={ 6 }  DS={ 10 }      n=2 acc=23 coef=4
RS={ 12 forth }  mode=ppolyc  PS={ 7 }  DS={ 10 }      n=1 acc=234 coef=5.5
RS={ 12 forth }  mode=ppolye  PS={ 8 }  DS={ 10 }      acc=2345.5
RS={ 12 }        mode=forth   PS={ 8 }  DS={ 2345.5 }  instr="EXIT"

  (Figure 11: a trace for the program in Figure 10)

The trace above does not show what &P(X) does; the effect of running &P(X) is to put the address of the beginning of data of the polynomial, namely, 3, into the data stack. Note how a polynomial - that in most other languages would be a piece of passive data - in Forth is represented as two programs, P(X) and &P(X), that share their data. Compare that with the situation of closures in Lua - two closures created by the same mother function, and referring to variables that were local to that mother function, share upvalues.

Here is another example. Let's write “=>” for “implies”, and “&” for “and”. Then this,

(Q=>R)=>((P&Q)=>(P&R))

  ( Figure 12a: a proposition. )

is a “formula”, or a “proposition”, in Propositional Calculus; incidentally, it is a tautology, i.e., always true.

In some situations, for example, if we want to find a proof for that proposition, or if we want to evaluate its truth value for some assignment of truth values to P, Q, and R, we need to refer to subformulas of that formula. If we represent it in bytecode using Polish Notation (not Reverse Polish Notation! Can you see why?) then this becomes trivial:

memory = { "=>", "=>", "Q", "R", "=>", "&", "P", "Q", "&", "P", "R" }
      --   1     2     3    4    5     6    7    8    9    10   11
   ( Figure 12b: the proposition in Figure 11 in Polish Notation. )

Subformulas can now be referred to by numbers - the position in the memory where they start. We can write a word to parse a proposition starting at some position in the memory; if that position contains a binary connective like “=>” or “&”, then that word calls itself two times to parse the subformulas at the "left" and at the "right" of the connective. If the word memoizes the resulting structure by storing it in a table formulas, then re-parsing the formula that starts at the position, say, 6, becomes very quick: the result is formulas[6], and the pointer should be advanced to formulas[6].next. Figure 13 shows the contents of that table after parsing the formula that starts at memory[1].

1:  { addr=1, cc="=>", l=2,  r=5,  next=12, name="((Q=>R)=>((P&Q)=>(P&R)))" }
 2: { addr=2, cc="=>", l=3,  r=4,  next=5,  name="(Q=>R)" }
 3: { addr=3,                      next=4,  name="Q" }
 4: { addr=4,                      next=5,  name="R" }
 5: { addr=5, cc="=>", l=6,  r=9,  next=12, name="((P&Q)=>(P&R))" }
 6: { addr=6, cc="&",  l=7,  r=8,  next=9,  name="(P&Q)" }
 7: { addr=7,                      next=8,  name="P" }
 8: { addr=8,                      next=9,  name="Q" }
 9: { addr=9, cc="&",  l=10, r=11, next=12, name="(P&R)" }
10: { addr=10,                     next=11, name="P" }
11: { addr=11,                     next=12, name="R" }

  ( Figure 13: the table "formulas" (for Figure 12b). )

The parser for the language for Propositional Calculus in the last section had to be recursive, but it didn't need backtracking to work. Here is a language that is evidently useful - even if at this context it looks like an academic exercise - and whose parser needs a bit of backtracking, or at least lookahead. Consider the following program in Lua:

foo = function ()
    local storage
    return function () return storage end,
           function (x)   storage = x end
  end

  -- ( Figure 14 )

It can be represented in bytecode in miniforth as:

memory = {
  "foo", "=", "function", "(", ")",
      "local", "storage",
      "return", "function", "(", ")", "return", "storage", "end", ",",
                "function", "(", "x", ")", "storage", "=", "x", "end",
    "end",
  "<eof>" }

  -- ( Figure 15 )

One way of “executing” this bytecode made of string tokens could be to produce in another region of the memory a representation in Lua of the bytecode language that the Lua VM executes; another would be to convert that to another sequence of string tokens - like what MetaLua ([Fleutot]) does. Anyway, there's nothing special with our choice of Lua here - Lua just happens to be a simple language that we can suppose that the reader knows well, but it could have been any language. And as these parsers and transformers would be written in Lua, they would be easy to modify.

Caveat lector: there is no single definition for what is “Forth”... around 1994 the community had a big split, with some people working to create an ANSI Standard for Forth, and the creator of the language and some other people going in another direction, and not only creating new Forths that went against ideas of the Standard, but also stating that ANS Forth “was not Forth”. I can only write this section clearly and make it brief if I choose a very biased terminology; and also, I'm not going to be historically precise, either - I will simplify and distort the story a bit to get my points across. You have been warned!

Forth was very popular in certain circles at a time when computers were much less powerful than those of today. Some of the reasons for that popularity were easy to quantify: compactness of programs, speed, proximity to machine code, simplicity of the core of the language - i.e., of the inner and the outer interpreters. None of these things matter so much anymore: computers got bigger and faster, their assembly languages became much more complex, and we've learned to take for granted several concepts and facilities - malloc and free, high-level data structures, BNF - and now we feel that it is "simpler" to send characters through stdout than poking bytes at the video memory. Our notion of simplicity has changed.

Int the mid-90s came the ANS-Forth Standard, and with it a way to write Forth source that would run without changes in Forths with different memory models, on different CPU architectures. At about the same time the creator of the language, Chuck Moore, started to distance himself from the rest of the community, to work on Forths that were more and more minimalistic, and on specialized processors that ran Forth natively.

My experience with (non-Chuck-Moore-) Forth systems written before and after the ANS Standard was that in the pre-ANS ones the format of the bytecode was stated clearly, and users were expected to understand it; in Forths written after the Standard the bytecode was not something so mundane anymore - it became a technical detail, hidden under abstractions.

Old Forths were fun to use. When I was a teenager I spent hundreds of evenings playing with Forths on an IBM-PC - first FIG-Forth and MVP-Forth, then HS-Forth, a commercial Forth whose memory model (8086 machine code, dictionary and Forth definitions in different memory segments, indirect-threaded, no primitives, multiple heads) inspired some of the ideas in this paper. At one point I spent some weeks writing a program that constructed a "shadow image" of the Forth segment, with a letter or a number for each byte in a head, a "." for each byte in a Forth instruction, "_"s and "$"s for bytes in literal numbers and strings, "<"s and ">"s for the bytes that were addresses in backward or forward jumps (i.e., the two bytes following each call to BRANCH or 0BRANCH) - and spaces for the unknown bytes, as I didn't have the source for the whole core system, and some words were tricky to decompile... Then I printed the result, in five pages, each with a grid of 64x64 characters, and addresses at the borders; that gave me a map of all the bytes in words in the core system that were not defined in assembly language.

I've met many people over the years who have been Forth enthusiasts in the past, and we often end up discussing what made Forth so thrilling to use at that time - and what we can do to adapt its ideas to the computers of today. My personal impression is that Forth's main points were not the ones that I listed at the beginning of this section, and that I said that were easy to quantify; rather, what was most important was that nothing was hidden, there were no complex data structures around with “don't-look-at-this” parts (think on garbage collection in Lua, for example, and Lua's tables - beginners need to be convinced to see these things abstractly, as the concrete details of the implementation are hard), and everything - code, data, dictionaries, stacks - were just linear sequences of bytes, that could be read and modified directly if we wished to. We had total freedom, defining new words was quick, and experiments were quick to make; that gave us a sense of power that was totally different from, say, the one that a Python user feels today because he has huge libraries at his fingertips.

A Forth-like language built on top of Lua should be easier to integrate with the rest of the system than a "real" Forth written in C. Also, it's much easier to add new syntaxes and bytecode languages to a mode-based Forth than to a conventional one. And we are not forced to store only numbers in the memory; we can store also strings - I've used strings for primitives and heads here because this makes programs more readable -, or any other Lua objects, if we need to.

I do not intend to claim that miniforth is compact - in terms of memory usage -, or efficient, or useful for practical applications. But the natural ways for doing things in Forth were different from the ways that are natural in today's systems; and I believe that miniforth can be used to give to people glimpses into interesting ways of thinking that have practically disappeared, and that have become hard to communicate.

To Marc Simpson and Yuri Takhteyev for helpful discussions.

After a draft of this article had been written Marc Simpson engaged in a long series of discussions with me about Forths, Lisp, SmallTalk, several approaches to minimality, etc, and at one point, over the course of one hectic weekend in december, 2007, he implemented a usable (rather than just experimental) dialect of Forth - based mainly on Frank Sergeant's Pygmy Forth and Chuck Moore's cmForth, and borrowing some ideas from this article - on top of Ruby (“RubyForth”), and later ported his system to Python and C. A port of it to Lua is underway.

Jon Bentley: More Programming Pearls, Addison-Wesley, 1990 (chapter 9: Little Languages).

James T. Callahan: HS-Forth (program and manual). Harvard Softworks, 1986-1993.

Anton Ertl: Threaded Code. Retrieved from: http://www.complang.tuwien.ac.at/forth/threaded-code.html.

Brad Rodriguez: A BNF Parser in Forth. From: http://www.zetetics.com/bj/papers/bnfparse.htm.

Fabien Fleutot: MetaLua. At: http://metalua.luaforge.net/.

Kein-Hong Man: A No-Frills Introduction to Lua 5.1 VM Instructions.